Thinking in VertexPrograms
From the moment I saw this question in StackOverflow, I could mostly envision how it would work if I were to solve the problem with a custom VertexProgram in OLAP style. Unfortunately, this was not going to help the person who was asking the question because they were using Python and Neptune. It is not possible to write VertexProgram implementations in Python and Neptune doesn’t yet directly support a GraphComputer implementation to support it even if the implementation had been done on the JVM. Despite a VertexProgram not quite being the right answer, my mind was so locked into it, I had trouble considering the issue any other way and the Gremlin I was writing to try to get an answer reflected that.
Before progressing too much further, let’s cast some attention to the question. It presented an algorithm that involved calculating a “favor score” based on “weight” properties assigned to “favor” edges between “person” vertices. The sample graph looked like this:
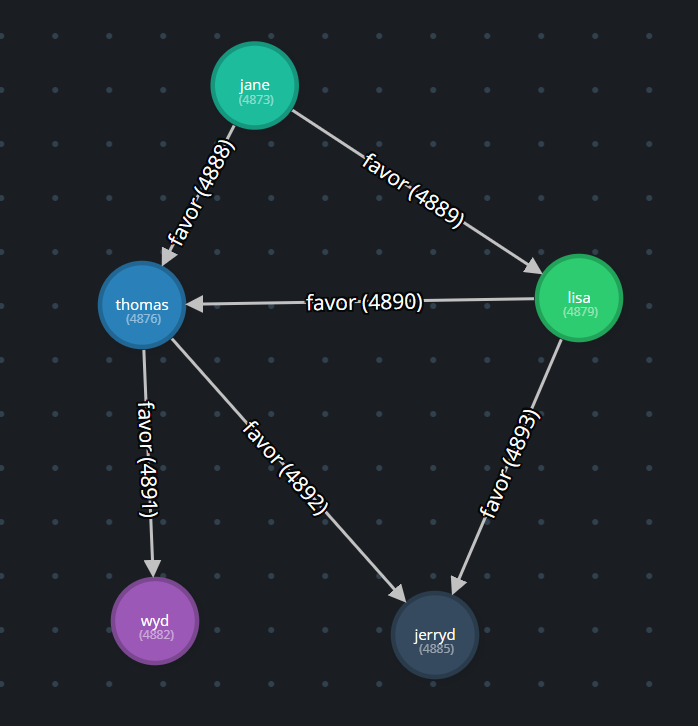Visualization by Gremlify.
and here is the script to generate it:
g.addV('person').as('1').
property(single, 'name', 'jane').
addV('person').as('2').
property(single, 'name', 'thomas').
addV('person').as('3').
property(single, 'name', 'lisa').
addV('person').as('4').
property(single, 'name', 'wyd').
addV('person').as('5').
property(single, 'name', 'jerryd').
addE('favor').from('1').to('2').
property('weight', 10).addE('favor').
from('1').to('3').property('weight', 20).
addE('favor').from('3').to('2').
property('weight', 90).addE('favor').
from('2').to('4').property('weight', 50).
addE('favor').from('2').to('5').
property('weight', 90).addE('favor').
from('3').to('5').property('weight', 100).iterate()The algorithm could be roughly explained as:
- From a starting vertex, sum the outgoing edge weights as
totalFavorand accept the value of an “incoming”currentFavoror use “1” if this is the starting vertex. - Traverse each outgoing edge and for each adjacent vertex calculate a “proportional favor” by multiplying the
currentFavorby the current edgeweightdivided bytotalFavor. This “proportional favor” is then added to the total for the adjacent vertex. - For each adjacent vertex recalculate favor starting from step 1 until there are no more paths to take.
The algorithm is a lot to take in as text and is more clearly expressed as code, so hopefully the examples to follow will help clarify what is happening. I’ve explained that my first instinct after reading this question pointed toward a VertexProgram, but knowing the answer would not satisfy the problem, my second instinct was that this algorithm was best implemented with sack()-step. While I couldn’t quite get that approach to work right, Kelvin Lawrence was good enough to produce the answer which was suprisingly elegant in its base form:
g.withSack(1).V().
has('person','name','jane').
repeat(outE().
sack(mult).
by(project('w','f').
by('weight').
by(outV().outE().values('weight').sum()).
math('w / f')).
inV().
simplePath()).
until(has('name','jerryd')).
sack().
sum()Unable to write the above query in the time I’d allowed myself, I figured I could at least get the VertexProgram approach out of my head and implement it as an alternative answer. As a first step to understanding this solution, it is important to gather an understanding of what a VertexProgram is and what its relation is to a GraphComputer. A GraphComputer is the heart of OLAP-style processing in TinkerPop, where unlike OLTP-style workloads which focus on processing a localized subset of the graph, OLAP instead focuses on large subsets of the graph or the entire graph. The GraphComputer is meant to help orchestrate the work of processing graph in bulk synchronous parallel style. The “work” is the VertexProgram in action, where we can think of the GraphComputer as copying the VertexProgram to each vertex in the graph for execution in parallel until the termination condition of the VertexProgram is met.
We tend to think of OLAP for large-scale graphs (on the order of billions of edges or more) which would typically imply the use of Spark and its GraphComputer implementation, but for learning purposes and perhaps some use cases this approach might make sense for TinkerGraphComputer. TinkerGraphComputer is designed to work with TinkerGraph and uses a thread pool to distribute work for parallel processing of the graph. In relation to the StackOverflow question, I’d envisioned a solution that would use Java to extract a subgraph() from Neptune and then with that subgraph as a TinkerGraph on the client, TinkerGraphComputer could be used to process the custom VertexProgram. There would potentially be some expense in the serialization cost for the subgraph, but depending on the size of that subgraph the execution of the TinkerGraphComputer running all in-memory would likely be quite fast.
There is a fair bit of boilerplate code to building a VertexProgram and perhaps that points to an area for improvement. With that concern aside, a VertexProgram begins as follows:
public class FavorVertexProgram implements VertexProgram<Double> {
}The <Double> generic declaration is meant to specify the type of the message that is passed from one vertex to the next. In this case, the Double refers to the “currentFavor” described in step 1 of the algorithm. Recall that VertexProgram is executed over and over again in parallel on each vertex until the termination condition is met. With that context in mind, think of the message passing as a way for those programs on each vertex to communicate with each other. Vertices send messages and receive messages by way of a Messenger and that object is made available in the VertexProgram by way of this method:
public void execute(Vertex vertex, Messenger<Double> messenger, Memory memory) {
}The execute() method is the core part of the VertexProgram lifecycle and typically where most of the logic for the VertexProgram resides. It is called by the GraphComputer worker for each iteration of the process until the termination requirements are met. In addition to the Messenger, the execute() method also supplies the current Vertex on which the program is running and an instance of the Memory of the GraphComputer which is a global data structure where vertices can share information. My implementation of this method looked like this:
public class FavorVertexProgram implements VertexProgram<Double> {
public static final String FAVOR = "^favor";
public static final String TOTAL_FAVOR = "^totalFavor";
private static final String VOTE_TO_HALT = "favorVertexProgram.voteToHalt";
private static final Set<MemoryComputeKey> MEMORY_COMPUTE_KEYS =
Collections.singleton(MemoryComputeKey.of(
VOTE_TO_HALT, Operator.and, false, true));
...
@Override
public void execute(Vertex vertex, Messenger<Double> messenger, Memory memory) {
// through Memory we can check how many times the VertexProgram has been
// executed. that might be useful in initializing some state or controlling
// some flow or determining if it is time to terminate. in this case the first
// pass is used to calculate the "total flavor" for all vertices and to pass
// the calculated current favor forward along to incident edges only for
// the "start vertex" - in the context of the question, this starting vertex
// would be "jane"
if (memory.isInitialIteration()) {
// on the first pass, just initialize the favor and totalFavor properties
boolean startVertex = vertex.value("name").equals(nameOfStartVertrex);
double initialFavor = startVertex ? 1d : 0d;
vertex.property(VertexProperty.Cardinality.single, FAVOR, initialFavor);
vertex.property(VertexProperty.Cardinality.single, TOTAL_FAVOR,
IteratorUtils.stream(vertex.edges(Direction.OUT)).
mapToDouble(e -> e.value("weight")).sum());
if (startVertex) {
Iterator<Edge> incidents = vertex.edges(Direction.OUT);
// if there are no outgoing edges then from the perspective of
// this VertexProgram, there is no need to process this
// VertexProgram any further. Setting the memory key of VOTE_TO_HALT
// to true will have the effect of saying that this vertex believes
// there is nothing more to do and therefore it's ok to stop
// executing. all vertices must agree to this halting and looking
// above to the MEMORY_COMPUTE_KEYS we can see that the VOTE_TO_HALT
// key is define using an Operate.and which will have the effect of
// ANDing together the votes of all vertices to set this key in Memory.
// As such, any one vertex that sets this key to false will negate
// the termination and only a unanimous setting of true will stop it.
memory.add(VOTE_TO_HALT, !incidents.hasNext());
// iterate all the outgoing edges and for each send a message to the
// adjacent vertex with the calculated "proportional favor"
while (incidents.hasNext()) {
Edge incident = incidents.next();
messenger.sendMessage(MessageScope.Global.of(incident.inVertex()),
(double) incident.value("weight") / (double) vertex.value(TOTAL_FAVOR));
}
}
} else {
// after the first iteration of the VertexProgram messages should be passing
// among vertices along outgoing edges. those messages received by the
// current vertex should be checked as they contain the incoming proportional
// favor that needs to be applied to it.
Iterator<Double> messages = messenger.receiveMessages();
boolean hasMessages = messages.hasNext();
// assuming there are messages to process, those proportional favors are
// summed together as described in step 2 of the algorithm
if (hasMessages) {
double adjacentFavor = IteratorUtils.reduce(messages, 0.0d, Double::sum);
vertex.property(VertexProperty.Cardinality.single, FAVOR,
(double) vertex.value(FAVOR) + adjacentFavor);
// the logic to follow is described above however we must now multiply
// the proportional favor by the adjacent favor before sending the
// message. technically, this could have been done above and this duplicate
// code likely extracted to a function - the adjacentFavor above just
// defaults to "1" and therefore has no effect on the calculation.
Iterator<Edge> incidents = vertex.edges(Direction.OUT);
memory.add(VOTE_TO_HALT, !incidents.hasNext());
while (incidents.hasNext()) {
Edge incident = incidents.next();
messenger.sendMessage(MessageScope.Global.of(incident.inVertex()),
adjacentFavor * ((double) incident.value("weight") / (double) vertex.value(TOTAL_FAVOR)));
}
}
}
}
}While the complete code for the FavorVertexProgram will be shown below, the above code is basically the translation of that Gremlin sack() implementation, thus taking us from OLTP to OLAP. Writing VertexProgram implementations requires a different style of thinking than simply writing a bit of Gremlin, yet both can encode the same algorithm. We see this notion evident in a number of the Gremlin Recipes, where we demonstrate both an OLTP and an OLAP approach to getting an answer and is best exemplified in the Connected Components and Shortest Path sections. It is important to figure out whether or not there is an advantage to taking one approach or the other given your use case.
In the context of the original question, I would think that the OLTP approach is best because it works with Neptune in the programming language of the user’s choice, does much of the heavy lifting with sack() which is typically quite efficient and I suspect the traversal itself is not global in nature. If this last point is not the case (issues with Neptune and Python aside), then OLAP may prove to be a better choice and we could likely adapt this FavorVertexProgram to calculate more than one favor set at a time, so rather than just consider “jane” we might do the same calculation in parallel for all the people in the graph.
The full FavorVertexProgram can be found below:
public class FavorVertexProgram implements VertexProgram<Double> {
public static final String FAVOR = "^favor";
public static final String TOTAL_FAVOR = "^totalFavor";
private static final String VOTE_TO_HALT = "favorVertexProgram.voteToHalt";
private static final Set<MemoryComputeKey> MEMORY_COMPUTE_KEYS = Collections.singleton(MemoryComputeKey.of(VOTE_TO_HALT, Operator.and, false, true));
private MessageScope.Local<?> scope = MessageScope.Local.of(__::outE);
private Set<MessageScope> scopes;
private Configuration configuration;
private String nameOfStartVertrex = null;
private FavorVertexProgram() {}
@Override
public void loadState(Graph graph, Configuration config) {
configuration = new BaseConfiguration();
if (config != null) {
ConfigurationUtils.copy(config, configuration);
}
nameOfStartVertrex = configuration.getString("name");
scopes = new HashSet<>(Collections.singletonList(scope));
}
@Override
public void storeState(Configuration config) {
VertexProgram.super.storeState(config);
if (configuration != null) {
ConfigurationUtils.copy(configuration, config);
}
}
@Override
public void setup(Memory memory) {
memory.set(VOTE_TO_HALT, true);
}
@Override
public void execute(Vertex vertex, Messenger<Double> messenger, Memory memory) {
// through Memory we can check how many times the VertexProgram has been
// executed. that might be useful in initializing some state or controlling
// some flow or determining if it is time to terminate. in this case the first
// pass is used to calculate the "total flavor" for all vertices and to pass
// the calculated current favor forward along to incident edges only for
// the "start vertex" - in the context of the question, this starting vertex
// would be "jane"
if (memory.isInitialIteration()) {
// on the first pass, just initialize the favor and totalFavor properties
boolean startVertex = vertex.value("name").equals(nameOfStartVertrex);
double initialFavor = startVertex ? 1d : 0d;
vertex.property(VertexProperty.Cardinality.single, FAVOR, initialFavor);
vertex.property(VertexProperty.Cardinality.single, TOTAL_FAVOR,
IteratorUtils.stream(vertex.edges(Direction.OUT)).
mapToDouble(e -> e.value("weight")).sum());
if (startVertex) {
Iterator<Edge> incidents = vertex.edges(Direction.OUT);
// if there are no outgoing edges then from the perspective of
// this VertexProgram, there is no need to process this
// VertexProgram any further. Setting the memory key of VOTE_TO_HALT
// to true will have the effect of saying that this vertex believes
// there is nothing more to do and therefore it's ok to stop
// executing. all vertices must agree to this halting and looking
// above to the MEMORY_COMPUTE_KEYS we can see that the VOTE_TO_HALT
// key is define using an Operate.and which will have the effect of
// ANDing together the votes of all vertices to set this key in Memory.
// As such, any one vertex that sets this key to false will negate
// the termination and only a unanimous setting of true will stop it.
memory.add(VOTE_TO_HALT, !incidents.hasNext());
// iterate all the outgoing edges and for each send a message to the
// adjacent vertex with the calculated "proportional favor"
while (incidents.hasNext()) {
Edge incident = incidents.next();
messenger.sendMessage(MessageScope.Global.of(incident.inVertex()),
(double) incident.value("weight") / (double) vertex.value(TOTAL_FAVOR));
}
}
} else {
// after the first iteration of the VertexProgram messages should be passing
// among vertices along outgoing edges. those messages received by the
// current vertex should be checked as they contain the incoming proportional
// favor that needs to be applied to it.
Iterator<Double> messages = messenger.receiveMessages();
boolean hasMessages = messages.hasNext();
// assuming there are messages to process, those proportional favors are
// summed together as described in step 2 of the algorithm
if (hasMessages) {
double adjacentFavor = IteratorUtils.reduce(messages, 0.0d, Double::sum);
vertex.property(VertexProperty.Cardinality.single, FAVOR,
(double) vertex.value(FAVOR) + adjacentFavor);
// the logic to follow is described above however we must now multiply
// the proportional favor by the adjacent favor before sending the
// message. technically, this could have been done above and this duplicate
// code likely extracted to a function - the adjacentFavor above just
// defaults to "1" and therefore has no effect on the calculation.
Iterator<Edge> incidents = vertex.edges(Direction.OUT);
memory.add(VOTE_TO_HALT, !incidents.hasNext());
while (incidents.hasNext()) {
Edge incident = incidents.next();
messenger.sendMessage(MessageScope.Global.of(incident.inVertex()),
adjacentFavor * ((double) incident.value("weight") / (double) vertex.value(TOTAL_FAVOR)));
}
}
}
}
@Override
public Set<VertexComputeKey> getVertexComputeKeys() {
return new HashSet<>(Arrays.asList(
VertexComputeKey.of(FAVOR, false),
VertexComputeKey.of(TOTAL_FAVOR, false),
VertexComputeKey.of(TraversalVertexProgram.HALTED_TRAVERSERS, false)));
}
@Override
public Set<MemoryComputeKey> getMemoryComputeKeys() {
return MEMORY_COMPUTE_KEYS;
}
@Override
public boolean terminate(Memory memory) {
boolean voteToHalt = memory.<Boolean>get(VOTE_TO_HALT);
if (voteToHalt) {
return true;
} else {
// it is basically always assumed that the program will want to halt, but if message passing occurs, the
// program will want to continue, thus reset false values to true for future iterations
memory.set(VOTE_TO_HALT, true);
return false;
}
}
@Override
public Set<MessageScope> getMessageScopes(Memory memory) {
return scopes;
}
@Override
public GraphComputer.ResultGraph getPreferredResultGraph() {
return GraphComputer.ResultGraph.NEW;
}
@Override
public GraphComputer.Persist getPreferredPersist() {
return GraphComputer.Persist.VERTEX_PROPERTIES;
}
@Override
@SuppressWarnings("CloneDoesntCallSuperClone,CloneDoesntDeclareCloneNotSupportedException")
public FavorVertexProgram clone() {
return this;
}
@Override
public Features getFeatures() {
return new Features() {
@Override
public boolean requiresLocalMessageScopes() {
return true;
}
@Override
public boolean requiresVertexPropertyAddition() {
return true;
}
};
}
public static FavorVertexProgram.Builder build() {
return new FavorVertexProgram.Builder();
}
// having a builder that constructs the Configuration object for the VertexProgram is helpful
// to ensure that it gets built properly and ensures a more fluent style of usages that is
// common in Gremlin
public static final class Builder extends AbstractVertexProgramBuilder<FavorVertexProgram.Builder> {
private Builder() {
super(FavorVertexProgram.class);
}
public FavorVertexProgram.Builder name(final String nameOfStartVertex) {
this.configuration.setProperty("name", nameOfStartVertex);
return this;
}
}
}This FavorVertexProgram can then be utilized as follows, where graph is a TinkerGraph with the sample data from the script at the start of this post:
ComputerResult result = graph.compute().program(
FavorVertexProgram.build().name("jane").create()).submit().get();
GraphTraversalSource rg = result.graph().traversal();
Traversal elements = rg.V().elementMap();
while(elements.hasNext()) {
System.out.println(elements.next());
}which would print:
{id=0, label=person, ^favor=1.0, name=jane, ^totalFavor=30.0}
{id=2, label=person, ^favor=0.6491228070175439, name=thomas, ^totalFavor=140.0}
{id=4, label=person, ^favor=0.6666666666666666, name=lisa, ^totalFavor=190.0}
{id=6, label=person, ^favor=0.23182957393483708, name=wyd, ^totalFavor=0.0}
{id=8, label=person, ^favor=0.768170426065163, name=jerryd, ^totalFavor=0.0}While most users won’t require a custom VertexProgram in the first days of days of their work with their TinkerPop graph system, the possibility for needing to use OLAP ends up looming quite quickly as a graph can grow at a suprising rate. In many cases, users can be satisfied by writing the Gremlin that they’ve grown accustomed to and executing it as a distributed traversal in OLAP.
gremlin> g = graph.traversal().withComputer(SparkGraphComputer)
==>graphtraversalsource[hadoopgraph[gryoinputformat->gryooutputformat], sparkgraphcomputer]
gremlin> g.V().count()
==>6
gremlin> g.V().out().out().values('name')
==>lop
==>ripplePerhaps users are not aware but when they do the above, their Gremlin is being executed by way of the TraversalVertexProgram which processes Gremlin steps in such a way so as to allow them to be executed in the GraphComputer model. This general purpose VertexProgram with the power of Gremlin can cover a massive set of large scale traversal use cases. For all other cases, it may be necessary to develop your own VertexProgram to solve your problems.